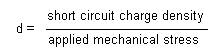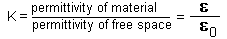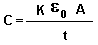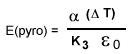Terminology

Introduction
Relationships
"d" Constant
"g" Constant
Dielectric Constants
Capacitance
Coupling Coefficients
Young's Modulus
Density
Dissipation Factor
Mechanical (Qm)
Curie Temperature
Aging Rate
Pyroelectricity
Performance

INTRODUCTION:	When a piezoceramic element is stressed electrically by a voltage, its dimensions change. When it is stressed mechanically by a force, it generates an electric charge. If the electrodes are not short-circuited, a voltage associated with the charge appears. A piezoceramic is therefore capable of acting as either a sensing or transmitting element, or both. Since piezoceramic elements are capable of generating very high voltages, they are compatible with today's generation of solid-state devices - rugged, compact, reliable, and efficient. The following text describes the terminology of piezoceramics and the relationship among variables for functional applications.
RELATIONSHIPS:	Relationships between applied forces and the resultant responses depend upon: the piezoelectric properties of the ceramic; the size and shape of the piece; and the direction of the electrical and mechanical excitation. To identify directions in a piezoceramic element, three axes are used. These axes, termed 1, 2, and 3, are analogous to X, Y, and Z of the classical three dimensional orthogonal set of axes. The polar, or 3 axis, is taken parallel to the direction of polarization within the ceramic. This direction is established during manufacturing by a high DC voltage that is applied between a pair of electroded faces to activate the material. In shear operations, these poling electrodes are later removed and replaced by electrodes deposited on a second pair of faces. In this event, the 3 axis is not altered, but is then parallel to the electroded faces found on the finished element. When the mechanical stress or strain is shear, the subscript 5 is used in the second place. Piezoelectric coefficients with double subscripts link electrical and mechanical quantities. The first subscript gives the direction of the electric field associated with the voltage applied, or the charge produced. The second subscript gives the direction of the mechanical stress or strain. Several piezoceramic material constants may be written with a "superscript" which specifies either a mechanical or electrical boundary condition. The superscripts are T, E, D, and S, signifying: T = constant stress = mechanically free E = constant electric field = short circuit D = constant electrical displacement = open circuit S = constant strain = mechanically clamped As an example, K^T₃ expresses the relative dielectric constant (K), measured in the polar direction (₃) with no mechanical clamping applied.
"d" CONSTANT:	The piezoelectric constants relating the mechanical strain produced by an applied electric field are termed the strain constants, or the "d" coefficients. The units may then be expressed as meters per meter, per volts per meter (meters per volt). It is useful to remember that large d_ij constants relate to large mechanical displacements which are usually sought in motional transducer devices. Conversely, the coefficient may be viewed as relating the charge collected on the electrodes, to the applied mechanical stress. d₃₃applies when the force is in the 3 direction (along the polarization axis) and is impressed on the same surface on which the charge is collected. d₃₁ applies when the charge is collected on the same surface as before, but the force is applied at right angles to the polarization axis. The subscripts in d₁₅ indicate that the charge is collected on electrodes which are at right angles to the original poling electrodes and that the applied mechanical stress is shear. The units for the d_ij coefficients are commonly expressed as coulombs/square meter per newton/square meter. When the force that is applied is distributed over an area which is fully covered by electrodes (even if that is only a portion of the total electrode) the units of the area cancel from the equation and the coefficient may be expressed in terms of change per unit force, coulombs per newton. To view the d_ij coefficients in this manner is useful when charge generators are contemplated, e.g., accelerometers.
"g" CONSTANT:	The piezoelectric constants relating the electric field produced by a mechanical stress are termed the voltage constants, or the "g" coefficients. The units may then be expressed as volts/meter per newtons/square meter. Output voltage is obtained by multiplying the calculated electric field by the thickness of ceramic between electrodes. A "33" subscript indicates that the electric field and the mechanical stress are both along the polarization axis. A "31" subscript signifies that the pressure is applied at right angles to the polarization axis, but the voltage appears on the same electrodes as in the "33" case. A "15" subscript implies that the applied stress is shear and that the resulting electric field is perpendicular to the polarization axis. High g_ij constants favor large voltage output, and are sought after for sensors. Although the g coefficient are called voltage coefficients, it is also correct to say the g_ij is the ratio of strain developed over the applied charge density with units of meters per meter over coulombs per square meter.
DIELECTRIC CONSTANT:	The relative dielectric constant is the ratio of the permittivity of the material, , to the permittivity of free space, 0, in the unconstrained condition, i.e., well below the mechanical resonance of the part.
CAPACITANCE:	Whereas the relative dielectric constant is strictly a material property, the capacitance is a quantity dependent on the type of material and its dimensions. Capacitance is calculated by multiplying the relative dielectric constant by the permittivity of free space(₀ = 8.9 x 10^-12 farads/meter) and electrode surface area, then dividing by the thickness separating the electrodes. Units are expressed in farads. K₃ is related to the capacitance between the original poling electrodes. K₁ is related to the capacitance between the second pair of electrodes applied after removal of the poling electrodes for the purposes of shear excitation. At frequencies far below resonance, piezoelectric ceramic transducers are fundamentally capacitors. Consequently, the voltage coefficients g_ij are related to the charge coefficients d_ij by the dielectric constant K_ias, in a capacitor, the voltage V is related to the charge Q by the capacitance C. The equations are: Q = CV d₃₃ = K^T₃ ₀g₃₃ d₃₁ = K^T₃ ₀ g₃₁ d₁₅ = K^T₁ ₀ g₁₅ At resonance, the dielectric constant will be reduced by the factor (l - k²) where k is the coupling coefficient of the mode in question.
COUPLING COEFFICIENTS:	Electromechanical coupling k₃₃, k₃₁, k_p, and k₁₅ describe the conversion of energy by the ceramic element from electrical to mechanical form or vice versa. The ratio of the stored converted energy of one kind (mechanical or electrical) to the input energy of the second kind (electrical or mechanical) is defined as the square of the coupling coefficient. or Subscripts denote the relative directions of electrical and mechanical quantities and the kind of motion involved. They can be associated with vibratory modes of certain simple transducer shapes; k₃₃ is appropriate for a long thin bar, electroded on the ends, and polarized along the length, and vibrating in a simple length expansion and contraction. k₃₁ relates to a long thin bar, electroded on a pair of long faces, polarized in thickness, and vibrating in simple length expansion and contraction. k_p signifies the coupling of electrical and mechanical energy in a thin round disc, polarized in thickness and vibrating in radial expansion and contraction. k₁₅ describes the energy conversion in a thickness shear vibration. Since these coefficients are energy ratios, they are dimensionless.
YOUNG'S MODULUS:	As with all solids, piezoelectric ceramics have mechanical stiffness properties described as Young's Modulus. Young's Modulus is the ratio of stress (force per unit area) to strain (change in length per unit length). Because mechanical stressing of the ceramic produces an electrical response which opposes the resultant strain, the effective Young's Modulus with electrodes short circuited is lower than with the electrodes open circuited. In addition, the stiffness is different in the 3 direction from that in the 1 or 2 direction. Therefore, in expressing such quantities both direction and electrical conditions must be specified. Y^E₃₃ is the ratio of stress to strain in the 3 direction at constant field E (electrodes shorted). Y^D₃₃ is the equivalent with the electrodes open circuited. Y^E₁₁ and Y^D₁₁ are the moduli in the 1 or 2 direction. Y ^E₅₅ and Y^D₅₅ are the ratios of shear stress to shear strain. Units are usually newtons/square meter. It should be clearly understood that the piezoceramic properties described above are defined for ideal shapes measured under ideal mechanical and electrical boundary conditions. When put to use under practical device operating conditions, the predicted performance is approached but seldom realized. Non-ideal shapes and non-ideal boundary conditions contribute to transduction losses due to such things as standing waves, interfering vibrational modes, pseudo-clamping, stray electric and dielectric resistances. Since the possibilities are infinite, the designer must evaluate each component under the use conditions for which it is intended.
DENSITY:	The ratio of the mass to volume in the material, expresses in kg/m³
DISSIPATION FACTOR:	A measure of the dielectric losses in the material-defined as the tangent of the loss angle or the ratio of parallel resistance to the parallel reactance, expressed in percent.
MECHANICAL (Qm):	The ratio of reactance to resistance in the equivalent series circuit representing the mechanical vibrating resonant systems. The shape of the part affects the value.
CURIE TEMPERATURE:	The temperature at which the crystal structure changes from a non-symmetrical (piezoelectric) to a symmetrical (non-piezoelectric) form, expressed in degrees Celsius.
AGING RATE:	Aging is the attempt of the ceramic to change back to its original state prior to polarization. Aging of piezoelectric ceramics is a logarithmic function with time. The aging rate defines change in the material parameters per decade of time, i.e., 1-10 days, 5-50 days, etc.
PYROELECTRICITY:	Piezoelectric materials are also pyroelectric. They produce electric charge as they undergo a temperature change. When their temperature is increased, a voltage develops having the same orientation as the polarization voltage. When their temperature is decreased, a voltage develops having an orientation opposite to the polarization voltage, creating a depolarizing field with the potential to degrade the state of polarization of the part. The maximum electric field which arises due to a temperature shift is: where E (pyro) is the induced electric field in volts/meter, α is the pyroelectric coefficient in Coulomb/°C meter ², ΔT is the temperature difference in °C, K₃ is the dielectric constant, and ε₀ is the dielectric permittivity of free space. For PZT piezoceramic, α is typically ~ 400x10^-6 coulomb/°C meter².
PERFORMANCE:	Deflection and Force: Piezoelectric actuators are usually specified in terms of their free deflection and blocked force. Free deflection, X(f), refers to displacement at a given voltage level without the actuator working against any external load. Blocked force, F(b), refers to the force exerted at a given voltage level when the actuator is not allowed to move. Since the force at maximum deflection is zero, all other values of simultaneous displacement and force (for a given voltage level) are determined by a line drawn between these points on a force versus deflection diagram. In practice, a bending motor must move a specified amount and exert a specified force, which determines its operating point on the force versus deflection diagram. Work is maximized when the deflection performed permits one half the blocked force to be developed. This occurs when the deflection equals one half the free deflection. For cantilevered bending motors, X(f) is approximated by observing the tip deflection after energizing "in air", and F(b) by holding a "stiff" force gauge against the tip during energization.

CHAPTER 2

Glossary

Bimorph	A common term for "bender" or flexure element. Two layers of piezoceramic with or without a center shim.
Capacitance (free)	Referring to capacitance measurement on piezoelectric sample, the capacitance value obtained with sample being totally free of mechanical constraint during measurement process.
Capacitance (clamped)	Referring to capacitance measurement on a piezoelectric sample, the capacitance value obtained with sample being totally constrained from motion (i.e., "clamped") during measurement.
Coercive Field	Relating to a uniform ferroelectric material, the electric field required to oppose and bring to zero the internal polarization.
Charge Constant (d)	see "d" Constant
Compliance (s)	see "s" Constant
Coupling Coefficient (k)	A dimensionless number related to the effectiveness of electrical to mechanical energy conversion in nonresonant piezoelectric devices.
Curie Temperature:	Temperature at which the crystal structure undergoes a phase change from non-symmetrical lattice (such as tetragonal) to symmetrical lattice (such as cubic). Drastic dielectric and piezoelectric coefficient changes accompany this phase change.
"d" Constant	The piezoelectric constant relating applied electric field to resultant strain (units of meters per volt).
Density	In reference to piezoceramics, the mass per unit volume of a fired ceramic body. High density is an important measure of the quality and uniformity of ceramic material because it indicates the absence of microscopic pores which weaken the ceramic and cause poling difficulties.
Dielectric Constant	see "K" Constant (capital "K"!)
Electrostrictive Materials	An important class of solid state motor materials which exhibit strains proportional to the square of the applied electric field strength. (By contrast piezoelectric materials exhibit strains directly proportional to the applied field strength.
Ferroelectric Materials	Class of crystalline materials which possess an internal polarization which can be reversed by an externally applied field, i.e., a crystalline material which can be poled. All of the commonly used piezoceramics are ferroelectric.
Flaw Detection	An early practical application of piezoelectrics, taking advantage of the fact that ultrasonic sound waves travel freely in a solid object (such as a steel girder) until they hit an air bubble or a structural flaw, at which point they reflect backwards and are detectable.
Frequency Constant	see "N" Frequency Constant.
"g" Constant	Piezoelectric coefficient relating the stress applied to a crystal to the resultant electric field in the crystal (units of volt meters per Newton).
"K" Constant (Dielectric Constant)	For a piezoceramic material, the ratio of its dielectric permittivity to the dielectric permittivity of free space (8.85 E -12 Farads per Meter).
Mechanical Q	Referring to both piezoelectric materials and non-piezoelectric materials - the INVERSE of the percentage of mechanical input energy which is converted to heat (the balance being stored as recoverable elastic energy). A material with Q = 100, when subjected to 1.00 Joules of work, will lose .01 Joules to internal heating.
"N" Frequency Constant	Referring to resonating piezoelectric bodies of various geometries - the product of the resonant frequency and the length of the body along the axis of motion for the designated vibrational mode.
Piezo Electricity	An observed phenomenon in some crystals - the generation of surface charges in response to applied stresses.
Pyroelectricity	An observed phenomenon in some crystals - the generation of surface charges in response to the application of uniform temperature changes.
"s" Constant (compliance)	In an elastic body, the ratio of uniaxial strain to uniaxial stress.
Saw Device	Piezoelectric acoustic device employing surface acoustic waves.
Sonar	Name given to piezoelectric application consisting of measuring distances to submerged objects by broadcasting a sound "pulse" and timing the reflected signal.
Strain	The ratio of change-in-length to length. Used in describing the effects of applied stresses or applied electric fields.
Stress	In a mechanical sample, the ratio of applied force to cross-sectional area which bears that force.
Ultrasonic	Refers to the frequency of operation of an electric or acoustic device - a general term for "higher than 20 kiloherz".
Voltage Constant (g)	see "g" constant.
Young's Modulus	Elastic modulus of a solid sample, i.e., the ratio of stress in a sample to applied strain. For practical purposes, Young's modulus is equal to the inverse of the appropriate "s" constant.

CHAPTER 3

List of Symbols

Symbol	Name	Unit
A	Area	m²
C	Capacitance	F
D	Diameter	m
Di *	Dielectric displacement	C / m²
d_ij *	Piezoelectric charge constants	C / N
E_i *	Electric field components	V / m
E_c	Coercive field	V / m
F_r	Resonant frequency	Hz
F	Force	N
F_b	Blocking force	N
g_ij *	Piezoelectric voltage constants	V m / N
G	Shear modulus	N / m²
k	Electromechanical coupling coefficient
k₃₃	Longitudinal coupling coefficient
k₃₁	Transverse coupling coefficient
k₁₅	Shear coupling coefficient
k_p	Planar coupling coefficient
k_t	Thickness coupling coefficient
k_eff	Effective coupling coefficient
K_ij^S *	Relative dielectric constant at constant strain
K_ij^T *	Relative dielectric constant at constant stress
L	Length	m
p	Pressure	N / m²
ρ	Pyroelectric coefficient	C / m² K
Pi	Polarization components	C / m²
P	Power	W
Q	Mechanical quality factor
Q	Electric charge	C
Q_s	Short circuit charge	C
R	Electrical resistance	Ω
s_ij^E *	Elastic compliance at constant E	m² / N
S_i	Strain components
S_max	Maximum recommended strain
t	Time	s
t	Thickness	m
tr	Response time	s
T	Thickness	m
T_i *	Stress components	N / m²
V	Volume	m³
V	Electrical voltage	V
V_o	Open circuit voltage	V
v_s	Velocity of sound	m / s
x	Deflection	m
x_o	Free deflection	m
α	Thermal expansion coefficient	1 / K
ε_o	Dielectric constant of free space	F / m
ρ	Density	kg / m³
ρ	Electrical bulk resistivity	Ω m
* i = 1 to 3 * j = 1 to 6